Support Vector Machines: Part 1

6 min readOct 28, 2018

Support Vector Machines are a very popular class of machine learning algorithms which can be used for either classification or regression problems.

In this post, we will discuss some mathematical equations along with some code to understand how SVMs work.

Why do we need SVMs when we have some pretty good linear classifiers like logistic regression and perceptrons out there?

We discussed a few problems related to Perceptrons in the last post. Check this post to find out.

Let us continue discussing some of the problems related to perceptrons.

Which hyperplane fits the data best for this problem?

If you remember, a single layer perceptron will either use the blue separating line or the yellow separating line and will not bother to find the optimal hyperplane. Let us see how support vector machines will help us get the optimal line.

Support Vector Machines

Support Vector Machines are those classes of linear discriminant models which try to find the most optimal hyperplane for classifying the data. They can also be used for regression but we are not discussing that in this post. They use things called support vectors and margins. Let’s have a look at what those are.

Support Vectors and Margins

Support vectors are nothing but the points which are closest to the separating line from both the classes. The margin is the distance between those closest points and the separating line.

What SVMs want is to find the weights which maximise those margins (distances) between the classes and the separating line, as that would be the most optimal separating line. The farther the point from the separating line, the more confident we will be about the prediction for that particular point.

Mathematically, for some Δ, the equations of the line separating has two margins, one on the left and one on the right, as follows:

Ideally, the support vectors should lie on these lines. The classes have been made 1 and -1 for convenience.

Hyperplane:
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ambient space. If a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines.

Margins: Mathematical Definition

We know that the distance of any point x from a hyperplane Σwᵢxᵢ is given by

The total margin on either side of the separating line will be 2Δ. The equation for the distances can then be written as:

For the positive half, where y = +1:

For the negative half, where y = -1:

where we have separated the bias term from the w term for clarity.

These two inequations can be combined based on the y value of the examples and written as:

which can further be written as:

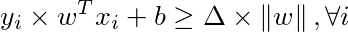
We can rescale the equation by setting, for a simpler solution:

Choosing this normalisation of the weights and bias we get the equation for boundaries as:

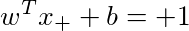
These will be the equations satisfied by the support vectors when the margin is equal to 2/ǁwǁ (the distance between the two equations given above) where the norm is L2-norm.

How do we get the best hyperplane from this equation?

Optimisation & Lagrange Multipliers

Now the problem is to get such weights which maximise this margin subject to the constraint given by the inequation which was derived earlier.

This maximisation problem is non-convex. This implies that we cannot solve it using something like gradient descent.

We can change this maximisation problem to a minimisation problem by taking an inverse and squaring it (as the weights which minimise ǁwǁ will also minimise its square). We are doing this because we want the function that we are minimising to be convex so as to reach a global minimum.

Now, we have:

This is an optimisation problem with some given constraint. If we want to use gradient descent to optimise this, we need to somehow incorporate this constraint into the function that we are trying to optimise. This can be done using Lagrange Optimisation.

Lagrange optimisation uses a concept called Lagrange multipliers, which is basically adding the constraint to the equation after multiplying it with Lagrange multipliers after converting the constraint to a “standard” form. Basically for some function f which is to be minimised, and a constraint g>=0, we have the function f-λg=0. More on optimisation will be covered in another article.

For this problem, the equation will be:

This function is convex too. The proof is beyond the scope of this article. Read more on Lagrange multipliers and convex functions if you’re interested.

All that is left to do is find the optimal values for this function L by deriving equations from the partial derivatives and finding the optimal lambda values and x values and we will be done.

Finding the optimal values can also be done through some numerical optimisation method like gradient descent.

The code, however, does not use this optimisation and uses simple if else to check for constraints and optimises the weights accordingly. It goes as follows:

This section of code just separates the two classes into two arrays and finds the extreme coordinates in maxval and minval of the positive and negative arrays. The learning rate is set to 0.01*maxval.

The second section of code is:

This section of code is the most important part where we train the model to classify the classes correctly. The comments explain the code efficiently. Basically, we try to reduce the weights by learning rate so as to reach the optimal point. This is why we initialise the weights to be half of the maximum value. If you have any doubts regarding this portion, please feel free to ask in the comments.

The last section of code is for visualisation and gives this output for our current data.

The inspiration for the code has been taken from this site: https://www.pythonprogramming.net, specifically from https://pythonprogramming.net/svm-optimization-python-machine-learning-tutorial/

Conclusion

Thank you for reading. This ends the first part of our discussion on SVMs.

A few questions, however, can still be raised:

What happens if the margins are too tight? (Overfitting)
What if the data is not linearly separable?

We haven’t answered these questions, yet. There are things like: Constrain Violations, Lagrange Duality and Kernel Trick, which will be discussed in part 2 of the discussion. To be able to describe the hyper-parameters: C and lambda, a good understanding of these topics is needed. Stay tuned to find out. ;)

Some good links related to SVMs:

Note: Kindly comment if you find any errors in here.